2024. 10. 13. 00:48ㆍProgramming Language/C
16-1 다차원 배열의 이해와 활용
다차원 배열은 2차원 배열과, 3차원 배열을 의미한다.
문법적으로는 4차원 배열이 있는데 이는 현실에 4차원 배열을 표현해야할 이유가 없기 때문에 사용되지 않는다.
거기서도 보통은 2차원 배열이 대부분이고 3차원 배열은 거의 사용되지 않는다.
먼저 2차원 배열은 1차원 배열이 여러개 합쳐져 있는 형태를 띄고 그 선언 방법은
int arr[3][5];와 같이 선언을 한다.
여기서 3부분은 5의 길이를 갖는 배열의 갯수가 3개가 합쳐진 형태임을 의미한다.
그냥 쉽게 생각하면
int arr[배열의 갯수][배열의 길이];라고 생각하면 된다.
이때 값에 접근하는 방법은
printf("%d", arr[1][3]);와 같이 접근이 가능하고 이것의 의미는 2번째 배열의 4번째 요소에 접근한다는 의미로 보면 된다.
이 내용을 정리해보자.
2차원, 3차원 배열 OK, 4차원, 5차원 배열 NO
int arrOnDim[10]; // 길이가 10인 1차원 int 배열
int arrTwoDim[5][5]; // 가로, 세로의 길이가 각각 5인 2차원 int형 배열
int arrThreeDim[3][3][3]; // 가로, 세로, 높이의 길이가 각각 3인 3차원 int 배열과 같이 선언이 가능하고 이 형태는
1차원 배열

2차원배열

3차원배열

의 형태를 띈다.
그런데 문법적으로 4차원 배열, 5차원 배열을 선언할 수 있는데 사용하지 않는 이유는 뭘까?
그건 현실에서 이를 사용하기 위해서 개념을 적용할 만한 것이 없기 때문에 활용이 되지 않기 때문이다.
다차원 배열을 의미하는 2차원 배열의 선언
2차원 배열의 선언 방식은
type 배열의 이름 [배열의 갯수][배열의 길이];와 같이 선언하면 된다.


이걸로 정확하게 그렇다!는 아니지만 유추해볼 만 한 내용인게 arr1의 경우는 4의 길이를 가진 3개의 배열을 합쳤기에
4 * 3 * 4(타입의 데이터 크기)를 했을때 나오는 값이 48인것을 알 수 있고 arr2의 경우는 9 * 7 * 4를 했을때 252가 나오는 것을 보면서 배열이 우리가 예상한대로 생성되었음을 알 수 있고 어떤 형태를 가질지도 알수 있다..
2차원 배열요소의 접근
2차원 배열 요소에 접근하는 방법은 그냥 배열과 동일한 방식을 사용한다.
배열의 요소에 접근할 때 실제 n번째 요소에 접근하기 위해서는 인덱스를 n-1을 사용했던 방식이 그대로 적용 되어 있다.
n번째 배열의 m번째 요소에 접근하고자 한다면
arr[n-1][m-1];과 같이 접근해야 한다는 것이다.
2차원 배열의 메모리상 할당의 형태
그런데 사실 2차원 배열이라고 메모리에서 2차원의 형태를 가지고 있는 것은 아니다.
실제 메모리는 1차원 형태로 주소값에 저장된다.

그렇기에 이 코드를 실행했을때 a[0][3]과 a[1][0]의 차이가 타입의 크기인 4가 나면서 연속적으로 구성되어 있는 것을 확인한다면

이는 메모리 공간에서는 실제고 그냥 나란히 할당되어 있음을 확인할 수 있는 증거이다.
이 주소값은 사실 물리적인 메모리의 주소값은 아니다.
사실상 하드웨어인 메모리에 주소값을 메기고 사용하는 주체는 OS이다.
그리고 그 메모리에 어떤 주소값을 메기고 어떻게 사용할지 또한 OS가 알아서 해주는 것이다
그렇기에 OS가 어떻게 메모리를 표현하고 어떻게 접근할 지가 중요한데 운영체제는 메모리를 그냥 주소값을 일렬로 plat한게 1차원적으로 매겨서 사용한다.
그러면 우리가 작성한 저 2차원 배열을 1차원 공간에서 표현하고 인식하고 사용할 수 있을까.
이건 운영체제도, 하드웨어 메모리도 아닌 컴파일러가 해주는 기능이다.
2차원 배열을 우리가 생성, 할당 하면, 이 2차원 배열을 1차원 형태로 할당하도록 다 변환하는것 또한 컴파일러이다.
또한 2차원 배열로 접근을 1차원의 형태로 변경해서 2차원 배열로 접근하는 것처럼 보여주는 것 또한 컴파일러이다.
그래서 Program => compiler => 메모리의 변환은 중간에서 컴파일러가 많은 일을 해준다.
2차원 배열의 선언과 동시에 초기화하기
int arr[3][3] = {
{1, 2, 3},
{4, 5, 6},
{7, 8, 9}
}
와 같이 초기화 리스트 안에는 행 단위로 초기화할 값들을 별도의 중괄호로 작성해주면 된다.
혹시
int arr[3][3] = {
{1},
{4, 5},
{7, 8, 9}
}와 같이 선언한다면 실제 생성되는 형태는
int arr[3][3] = {
{1, 0, 0},
{4, 5, 0},
{7, 8, 9}
}으로 길이가 맞지 않는 경우 앞부터 채우고 나머지는 0으로 초기화해준다.
여기서 만약
int arr[3][3] = {
1, 2, 3,
4, 5, 6,
7
}처럼 별도로 중괄호로 묶지 않는다면 왼쪽 위부터 시작해서 순서대로 초기화를 한다.
그렇게 해서 남아 버린 빈 공간은 0으로 채워준다.
int arr[3][3] = {
1, 2, 3,
4, 5, 6,
7, 0, 0
}
배열의 크기를 알려주지 않고 초기화하기
배열의 크기를 두개 모두 비워버리면 컴파일러가 채워넣을 숫자를 결정하지 못한다.
int arr[][] = {1,2,3,4,5,6,7,8}
배열의 중괄호에서 생략이 가능한 것은 배열의 갯수부분 만 생략이 가능하고 배열의 길이 부분은 생략할 수 없다.
int arr1[][4] = {1, 2, 3, 4, 5, 6, 7, 8}; // 컴파일 가능, 사용도 가능
int arr2[2][] = {1, 2, 3, 4, 5, 6, 7, 8}; // 컴파일 에러
배열의 갯수만 생략하면 컴파일러가 알아서
int arr1[2][4] = {1, 2, 3, 4, 5, 6, 7, 8};와 같이 초기화된 값을 확인해서 배열의 갯수를 계산해서 자동으로 생성해준다.
16-2 3차원 배열
3차원 배열의 경우는 2차원 배열이 여러개 모여있는 형태로 되어 있다.
현실과 동일하게 1차원 배열의 경우는 선, 2차원 배열의 경우는 선이 모여만들어진 평면, 3차원 배열의 경우는 평면이 모여 만들어진 입체라고 이해하면 될듯하다.
강의에선
int arr[높이(깊이)][세로][가로];이를 높이(깊이), 세로, 가로 라고 표현하는데 나는 이게 확 와닫는 개념은 아니기에 내가 해석 한대로 말해보자면
int arr[2차원 배열의 갯수][1차원배열의 갯수][배열의 길이];라고 표현할 것 같다.
역순으로 마지막에 들어가는 크기는 배열 하나의 길이를 의미하고, 두번째는 이 배열이 몆개가 모여서 2차원 배열을 형성했는지에 대한 숫자가 들어간다.
첫번째로 들어가는 크기는 마지막에 들어가는 길이의 배열이 두번째로 들어가는 숫자만큼 모여 만들어진 2차원 배열 몇개로 구성된 3차원 배열인지에 대한 숫자가 들어간다.
이 3차원 배열에 접근하는 방법 또한 다르지 않다.
만약 우리가 n번째 2차원 배열에 있는 m번째 배열의 k번째 요소에 접근하고자 한다면
printf("%d", arr[n-1][m-1][k-1]);과 같이 사용하면 된다.
3차원 배열의 논리적 구조
3차원 배열은 큐브와 같은 입체 구조를 갖고 있다.

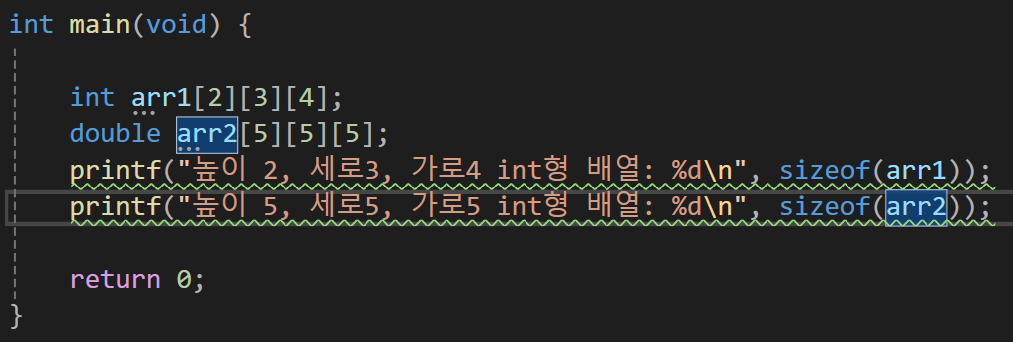

이 내용을 봤을때 이차원 배열과 동일하게 우리가 생성한 3차원 배열의 크기를 보면서 그 형태를 가늠하고 있는데 arr1의 경우는 2 * 3 * 4 * 4(int의 크기)로 96이 나오고, arr2의 경우는 5 * 5 * 5 * 8(double의 크기)로 1000이 나오는 것을 보면서 그 형태가 우리가 계속 그려왔던 형태임을 추측할 수 있다는 것을 보여준다.
3차원 배열의 선언과 접근

선언과 동시에 초기화 하는 방법은 위와 같이 사용하면 된다.
가장 내부에 있는게 가장 마지막에 있는 숫자, 그 위의 중괄호 기준으로는 중앙에 있는 숫자, 그 위 중괄호 기준으로 최상위인 가장 첫번째 있는 숫자의 갯수에 매칭된다.

사용법은 동일하고, 이해하기가 어렵지 않을 것이다.
'Programming Language > C' 카테고리의 다른 글
| 열혈C - Chapter 18 다차원 배열과 포인터의 관계 (0) | 2024.10.18 |
|---|---|
| 열혈C - Chapter 17 포인터의 포인터 (0) | 2024.10.13 |
| 열혈C - Chapter 14 포인터와 함수에 대한 이해 (0) | 2024.10.09 |
| 열혈C - Chapter 13 포인터와 배열! 함께 이해하기 (0) | 2024.10.07 |
| 열혈C - Chapter 12 포인터의 이해 (0) | 2024.10.03 |